Особенность прямых расположенных в предметной плоскости:
В пространстве: Если в пространстве прямая принадлежит предметной плоскости, то ее ортогональная проекция на предметную плоскость совпадает с самой прямой.
На картине: Если в пространстве прямая принадлежит предметной плоскости, то перспективные проекции прямой и ее ортогональной проекции совпадают.

Следует запомнить:

Прямая широт - это прямая параллельная основанию картины.

На рисунке 1 показан аппарат проецирования и перспективный чертеж (картина) прямой а, принадлежащей предметной плоскости и параллельной картине (прямой широт).

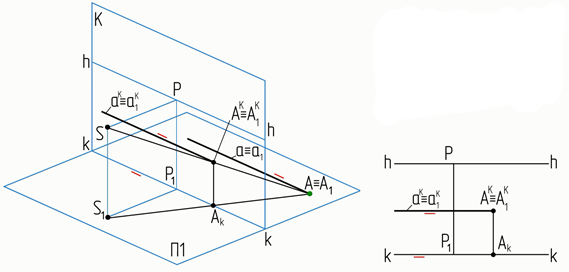
Рисунок 1. Перспектива прямых, расположенных в предметной плоскости параллельно картине

Особенность перспективы прямой широт расположенной в предметной плоскости:
Если в пространстве прямая принадлежит предметной плоскости и является прямой широт, то совпадающие перспективные проекции такой прямой и ее ортогональной проекции, расположены параллельно основанию картины и находятся между линией горизонта hh и основанием картины kk.

На рисунке 2 показаны слева направо иллюстрации (https://veniamin1.livejournal.com/311593.html) картин "Обучение коммерции" и "Доход" австро-венгерского художника еврейского происхождения Исидора Кауфмана (1853–1921) с указанием перспективы части прямых a, b, c и d, принадлежащих предметной плоскости и параллельных картине, и их ортогональных проекций a₁, b₁, c₁, d₁ этих прямых.

В пространстве:
Прямые a, b, c, d - прямые широт - это прямые, проходящие на полу (предметной плоскости) по линиям стыков половиц, расположеных параллельно основанию картины.
На картине:
Перспективы a^K, b^K, с^K, d^K прямых a, b, c, d расположены параллельно основанию картины kk между линией горизонта hh и основанием картины kk.
Перспективы a₁^K, b₁^K, c₁^K, d₁^K ортогональных проекций a₁, b₁, c₁, d₁, прямых a, b, c, d совпадают соответственно с перспективами a^K, b^K, c^K, d^K самих прямых a, b, c, d.

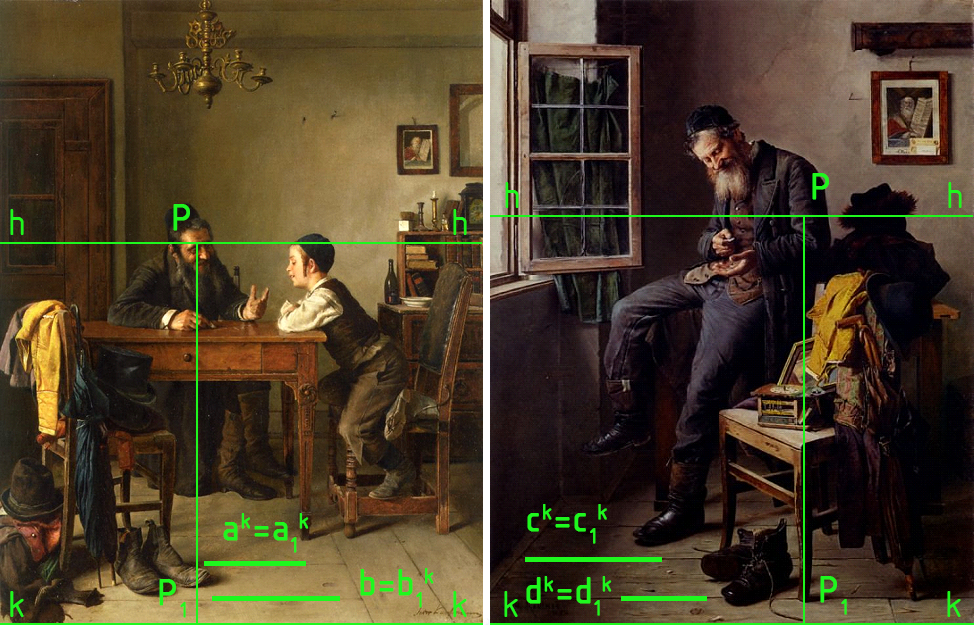
Рисунок 2. Перспектива прямых, расположенных в предметной плоскости параллельно картине

Наверх

Далее: к разделу "Перспектива прямых, расположенных
в предметной плоскости под произвольным углом к картине"